数式処理システムの Maxima で添え字つきの変数の和の微分などをしようとしたが、単純にはできなかった。調べるのに時間がかかったので、備忘録として残しておく。
調べたところ、stackoverflow の「Derivatives using indexed variables」に方法が書いてあった。
Kroneckerのdeltaの和を計算する sum_kron_delta.mac (https://pastebin.com/MmYJRqCq) と添え字付きの変数での和の微分を行う diff_sum.mac (https://pastebin.com/UGCPgvAn) を利用することで、添え字付きの変数の微分ができるようになる。
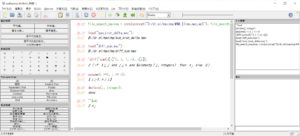
Windows10 の wxMaxima 20.06.6 で実行した例を次に示す。
目次
マクロのロード
上述のファイルをダウンロードして、ファイル名を sum_kron_delta.mac、diff_sum.mac としたとする。また、sum_kron_delta.mac、diff_sum.mac があるフォルダーを D:\Maxima\macro として説明する。
メニューからのロード
ファイルを読み込むためには、wxMaxima なら、メニューの「ファイル」→「パッケージ読み込み(L)…」をクリックして、ファイルを指定して読み込む。
sum_kron_delta.mac、diff_sum.mac の両方を読み込む。
コマンドでのロード
検索するディレクトリを追加
ちなみに、ロードするファイルのパスを設定するのは、wxMaxima なら、メニューの「Maxima」→「検索するディレクトリを追加」をクリックして、フォルダを指定しても良い。
ロード
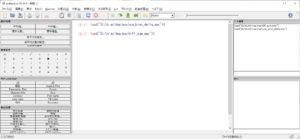
sum_kron_delta.mac、diff_sum.mac をロードするためには、次を実行する。
|
1 2 |
load("sum_kron_delta.mac"); load("diff_sum.mac"); |
微分の例
ここでは、「Derivatives using indexed variables」に書いてある例であるが、 \( \sum_{i=1}^n {x_i}^2 \) を \( x_j \) で微分して \( 2 x_j \) を得ることを考える。
微分
微分のためには、次を実行する。ここで、評価を抑制するために、diff や sumの前の ' (single quoate)が必要である。x[i] が \( x_i \) を表す。
|
1 |
'diff('sum(x[i]^2, i, 1, n), x[j]); |
これで、\( \sum_{i=1}^n {x_i}^2 \) を \( x_j \) を \( x_j \) で微分した結果が得られる。ただし、結果には、条件が含まれている。
条件
含まれている条件が取り除かれるように条件などを加える。
\( j \le 1, n \le j\) で、jが整数であることを次のように加える。
|
1 2 |
assume(j >=1, j <= n); declare(j, integer); |
単純化
追加の評価を行う " (double single quote) を使って単純化する。微分を行った式番号がたとえば5であったなら、"%o5 で式5の出力(o5)を単純化する。
直前の結果を単純化する場合には、"% を実行する。
微分のまとめ
以下のようにすれば、期待する結果 \( 2 x_j \) を得ることができる。以下の例では条件を先に加えている。
|
1 2 3 4 |
declare(j, integer); assume(j >=1, j <= n); 'diff('sum(x[i]^2, i, 1, n), x[j]); ''%; |